前言
每一个参与设计数据库表的人,都应该了解数据库范式。也许,你可以故意设计不符合第三范式(3NF)要求的数据库表,但前提是你应该知道什么是第三范式。
带着以下问题阅读本文,会更有收获哦!
- 什么是数据库范式?
- 为什么需要遵循某些范式?
- 怎么做才算遵循了范式?
- 什么时候不需要遵循范式?
当然,对于这里的每个问题,不会单独作为一节进行展开。下文的组织结构是,对每个范式逐一进行介绍,最后进行总结。在这个过程中,以上的几个问题自然就会解决。
什么是范式(NF)
按照教材中的定义,范式是 “符合某一种级别的关系模式的集合,表示一个关系内部各属性之间的联系的合理化程度”。
按我的理解,大概就是 数据库表的某种设计规范。而所谓“规范”,其实就是一条条规则。所以,只要把规则说得足够清晰、简洁、准确,自然而然就知道怎么用了。
数据库范式也分为1NF,2NF,3NF,BCNF,4NF,5NF。一般在我们设计关系型数据库的时候,最多考虑到BCNF就够。符合高一级范式的设计,必定符合低一级范式,例如符合2NF的关系模式,必定符合1NF。
下面逐一介绍每个范式。
基本概念
在正式开始之前,需要了解的最少必要概念:
- 表:如果用过 Excel,就很好理解了。所谓表,就类似 Excel 里的表格结构,每一列都代表一个属性,每一行都记录了一些数据。
- 比如,有一张成绩表,有这么几列 “学号、课程、分数”,而某一行形如 “ZY210388 数学 89”。
- 属性:参考 “表” 的定义,比如刚刚介绍的 “学号”。
- 属性组:包含几个属性的集合。所以,属性是特殊的属性组,即只包含一个属性的属性组。
- 记录:某一行数据。
- 函数依赖、码、主属性:对这几个概念的介绍参考下文,但可以先跳过,需要的时候再回过头来看。
函数依赖
若在一张存有数据的表中,在属性组 X 的值确定的情况下,属性 Y 的值也就唯一确定下来,那么就可以说 Y 函数依赖于 X,写作 X → Y。(速记:箭头的指向,就像是在说 X 经过推导/映射可以得到 Y)
也就是说,在数据表中,不存在任意两条记录,它们在 X 属性组上的值相同,而在 Y 属性上的值不同。X 确定了一个取值,Y 的取值也就确定下来,并且只有一个,不会有多个,就像函数映射 y = f(x) 一样,所以称作函数依赖。
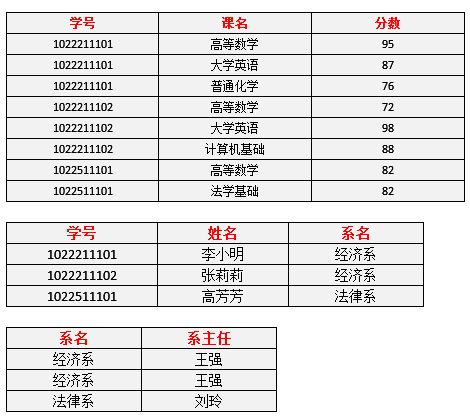
例如,对于表3中的数据,找不到任何一条记录,它们的学号相同而对应的姓名不同。所以我们可以说姓名函数依赖于学号,写作 学号 → 姓名。
表中其他的函数依赖关系还有如:
- 系名 → 系主任
- 学号 → 系主任
- (学号,课名) → 分数
但以下函数依赖关系则不成立:
- 学号 → 课名
- 学号 → 分数
- 课名 → 系主任
- (学号,课名) → 姓名
从“函数依赖”这个概念展开,还会有三个概念:
完全函数依赖
在一张表中,若 X → Y,且对于属性组 X 的任何一个真子集 X’(A 包含 B,而 B 不包含 A,则 B 是 A 的真子集),X’ → Y 不成立,那么我们称 Y 对于 X 完全函数依赖,记作 $X \overset{F}{\rightarrow} Y$。(速记:Full)
当我们说函数依赖时,一般暗指完全函数依赖。
例如:
- 学号 $\overset{F}{\rightarrow}$ 姓名
- (学号,课名) $\overset{F}{\rightarrow}$ 分数 (注:同一个的学号对应的分数不确定,同一个课名对应的分数也不确定,但确定下学号和课名后,分数就确定且唯一了)
部分函数依赖
假如 Y 函数依赖于 X,但同时 Y 并不完全函数依赖于 X,那么我们就称 Y 部分函数依赖于 X,记作 $X \overset{P}{\rightarrow} Y$。(速记:Partial)
Y 部分函数依赖于 X,意思是 Y 完全函数依赖于 X 的一部分(某个真子集),只需要这个子集,就能唯一确定下来 Y。显然,这意味着 X 必须是至少包含 2 个属性的属性组,才能存在非空的真子集。
例如:
- (学号,课名) $\overset{P}{\rightarrow}$ 姓名(因为 “学号 $\overset{F}{\rightarrow}$ 姓名”,只需要知道学号,不需要课名,也能知道姓名)
传递函数依赖
假如 Z 函数依赖于 Y,而 Y 函数依赖于 X (前提:『Y 不是 X 的子集,且 X 不函数依赖于 Y』),那么我们就称 Z 传递函数依赖于 X ,记作 $X \overset{T}{\rightarrow} Y$。(速记:Transfer)
码
设 K 为某表中的一个属性或属性组,若除 K 之外的所有属性,都完全函数依赖于 K(这个“完全”不要漏了),那么我们称 K 为候选码,简称为码。
通俗一点的理解:假如当 K 确定的情况下,该表(除 K 之外的)所有属性的值也就随之确定,那么 K 就是码。一张表中可以有超过一个码。实际应用中为了方便,通常选择其中的一个码作为主码。
例如:
对于表3,(学号、课名)这个属性组就是码。该表中有且仅有这一个码。(假设所有课没有重名的情况)
主属性
包含在所有码中的每个属性,都是主属性。而其他属性就是非主属性。
例如:
对于表3,主属性就有两个,学号 与 课名。
第一范式(1NF)
1NF 包含很多条规则,以某一条规则为例:符合 1NF 的表中的每个属性都不可再分。
网上对“不可再分”的解释,大多数我看了之后实在有点懵。按我的理解,所谓属性不可再分,指的是说,这个属性不应该有子属性。通俗来说就是,在存储某一行数据时,每个属性应该只存储一个属性值,而不存多个值。
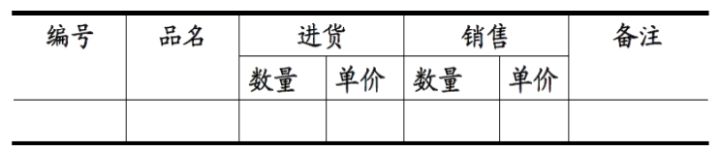
比如下表,你不能既要求有 “进货”、“销售” 这样的属性,又要求在 “进货” 这一属性下有两个子属性,存储两个值,分别表示进货的数量和单价。不能这么做。表 1:
要么,你的 “进货成本”、“销售收入” 属性下,都只存储一个值,事先计算好数量和单价的乘积存进来;
要么,你得把它拆成如下图所示的四列(“进货数量”、“进货单价”、“销售数量”、“销售收入”),表 2:
很多人可能会有个疑惑:怎么会有人想到要在表格中搞子属性呢?这不是脑子抽风了吗?
哈哈,之所以这么觉得,可能是因为你已经习惯了使用 MySQL 之类的数据库了。而所有的关系型数据库都不支持子属性这种骚操作,所以也就不会意料到还有人想这么搞。不过也正式因为数据库的这种限制,所有的表都自然而然已经满足第一范式。
那满足第一范式有啥好处?这个… 似乎不太好表述。我想,最大的好处就是简单吧。不把事情搞复杂,问题就简单多了。
反过来想,要是一个数据库表既有属性,也有子属性,那么在查询的时候,是按照属性来筛选呢,还是子属性呢?如果按照子属性,那属性还有存在的意义么?如果有子属性就不需要属性了,那还保留它干啥?如果要保留嵌套属性,那么数据库表底层的存储结构、查询逻辑等要怎么设计?思考一番你就会发现,似乎仅保留子属性比保留嵌套的属性带来的好处多得多。这也是为什么关系型数据库都这么设计。
第二范式(2NF)
1NF 存在的问题
仅仅满足第一范式的表长这样,表 3:

不用多想,最直接的观察就能想到这表存在一个问题:数据冗余。这里的姓名、系名、系主任等重复出现太多次了。
除此之外,细想一下,还有几个问题:
- 插入异常:假如学校新建了一个系,但是暂时还没有招收任何学生(比如3月份就新建了,但要等到8月份才招生),那么是无法将系名与系主任的数据单独地添加到数据表中去的。
- 修改异常:假如李小明转系到法律系,那么为了保证数据库中数据的一致性,需要修改三条记录中系与系主任的数据。
- 删除异常:假如将某个系中所有学生相关的记录都删除,那么所有系与系主任的数据也就随之消失了(一个系所有学生都没有了,并不表示这个系就没有了)。
所以你会发现,仅符合 1NF 的数据库设计,存在这样那样的问题。所以我们需要提高设计标准,去掉导致上述四种问题的因素,而这种设计标准,就是更高一级的范式(2NF)。使表设计符合第二范式,就是所谓的“规范化”。
2NF 的定义
2NF 的定义:在1NF的基础之上,消除了非主属性对于码的部分函数依赖。对 “函数依赖”、“码”、“非主属性”、与“部分函数依赖” 的解释,参考上文。
理解了 2NF 之后,就可以来看看怎么用它了。具体用法是,我们在设计好一个表时,或者拿到一个表结构时,先看看是否符合 2NF,如果不符合,再考虑怎么解决。
下面结合具体实例进行说明。在这个过程中,你会知道如何判断是否符合 2NF,如何重新设计表结构使之满足 2NF,以及满足 2NF 能带来哪些好处、解决哪些问题。
判断是否符合 2NF
首先,我们需要判断,表 3 是否符合 2NF 的要求?根据 2NF 的定义,其实就是要看数据表中是否存在 非主属性 对于 码 的 部分函数依赖。若存在,则数据表最高只符合 1NF 的要求,若不存在,则符合 2NF 的要求。
具体判断的步骤是:
第一步:找出数据表中所有的码。
第二步:根据第一步所得到的码,找出所有的主属性。那么,剩下的就都是非主属性了。
第三步:逐一检查每个非主属性,看是否对某个码存在部分函数依赖。
第一步:
- 查看所有每一单个属性,当它的值确定了,是否剩下的所有属性值都能确定。
- 查看所有包含有两个属性的属性组,当它的值确定了,是否剩下的所有属性值都能确定。
- ……
- 查看所有包含了六个属性,也就是所有属性的属性组,当它的值确定了,是否剩下的所有属性值都能确定。
看起来很麻烦是吧,但是这里有一个诀窍,就是假如A是码,那么所有包含了A的属性组,如(A,B)、(A,C)、(A,B,C)等,就都不是码了(因为此时必然有其它属性 Y 完全依赖于 A,进而必然是部分依赖于包含 A 的属性组,故这个属性组就不满足码得到要求了)。
图4表示了表中所有的完全函数依赖关系:
可以看到,能让所有其他属性都完全函数依赖的,只有 (学号, 课名) 这个属性组,因此它就是码。
第二步:
可以得到,主属性有两个:学号 与 课名;
非主属性有四个:姓名、系名、系主任、分数
第三步:
对于(学号,课名) → 姓名,有 学号 → 姓名,存在非主属性 姓名 对码(学号,课名)的部分函数依赖。
对于(学号,课名) → 系名,有 学号 → 系名,存在非主属性 系名 对码(学号,课名)的部分函数依赖。
对于(学号,课名) → 系主任,有 学号 → 系主任,存在非主属性 系主任 对码(学号,课名)的部分函数依赖。
综上,表 3 存在非主属性对于码的部分函数依赖,最高只符合 1NF 的要求,不符合 2NF 的要求。
使之符合 2NF
为了让表3符合2NF的要求,我们必须消除这些部分函数依赖,只有一个办法,就是将大数据表拆分成两个或者更多个更小的数据表,在拆分的过程中,要达到更高一级范式的要求,这个过程叫做”模式分解“。模式分解的方法不是唯一的,以下是其中一种方法:
选课表:(学号,课名,分数)
学生表:(学号,姓名,系名,系主任)
模式分解以后的新的函数依赖关系如图 5:
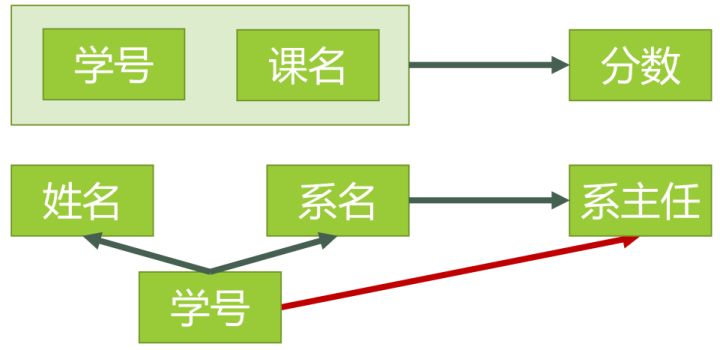
我们先来判断以下,选课表与学生表,是否符合了2NF的要求?
对于选课表,其码是(学号,课名),主属性是学号和课名,非主属性是分数。当学号确定,并不能唯一确定分数,当课名确定,也不能唯一确定分数,所以不存在非主属性分数对于码 (学号,课名)的部分函数依赖,所以此表符合 2NF 的要求。
对于学生表,其码是学号,主属性是学号,非主属性是姓名、系名和系主任,因为码只有一个属性,所以不可能存在非主属性对于码的部分函数依赖,所以此表符合 2NF 的要求。
表 4 展示了模式分解以后新的数据:

现在我们来看一下,进行同样的操作,是否还存在着之前的那些问题?
数据冗余:学生的姓名、系名与系主任,不再像之前一样重复那么多次了,但系主任和系名依然有些重复。——有改进,但不完全
插入异常:若要插入一个尚无学生的新系的信息,因为学生表的码是学号,不能为空,所以此操作不被允许。——无改进
修改异常:若李小明转系到法律系,只需要修改一次对应的系名的值即可。——有改进
删除异常:若删除某个系中所有的学生记录,该系的信息仍然全部丢失。——无改进
所以说,仅仅符合 2NF 的要求,很多情况下还是不够的,而出现问题的原因,在于仍然存在非主属性系主任对于码学号的传递函数依赖。为了能进一步解决这些问题,我们还需要将符合2NF要求的数据表改进为符合 3NF 的要求。
第三范式(3NF)
3NF 的定义
第三范式(3NF):3NF 在 2NF 的基础之上,消除了非主属性对于码的传递函数依赖。
判断是否符合 3NF
接下来我们看看表 4 中的设计,是否符合 3NF 的要求。
对于选课表,主码为(学号,课名),主属性为学号和课名,非主属性只有一个“分数”,不可能存在传递函数依赖,所以选课表的设计,符合 3NF 的要求。
对于学生表,主码为学号,主属性为学号,非主属性为姓名、系名和系主任。因为 学号 → 系名,同时 系名 → 系主任,所以存在非主属性系主任对于码学号的传递函数依赖(参考上文图 5 中的红色箭头),所以学生表的设计,不符合3NF的要求。
使之符合 3NF
为了让数据表设计达到3NF,我们必须进一步进行模式分解:
选课(学号,课名,分数)
学生(学号,姓名,系名)
系(系名,系主任)
再次分析是否都满足 3NF 要求:
对于选课表,符合 3NF 的要求,之前已经分析过了。
对于学生表,码为学号,主属性为学号,非主属性为姓名、系名,且二者间不存在函数依赖关系,所以不存在非主属性对于码的传递函数依赖,符合 3NF 的要求。
对于系表,码为系名,主属性为系名,非主属性只有一个系主任,不可能存在非主属性对于码的传递函数依赖(至少要有三个属性才可能存在传递函数依赖关系),所以符合 3NF 的要求。
新的函数依赖关系如图 6:
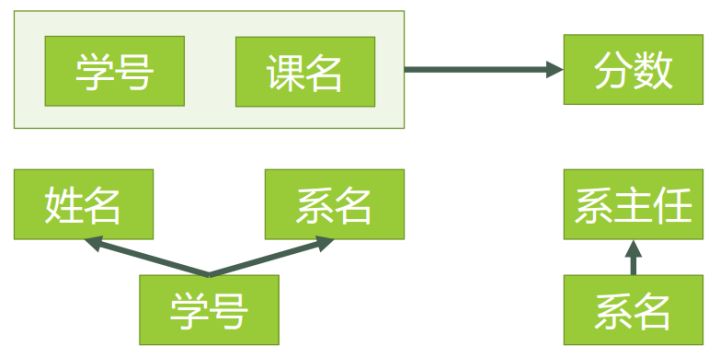
新的数据表如表 5:
注:上图中的系表,第二行重复了,有误,实际应去掉。
现在我们再来看一下,进行同样的操作,是否还存在着之前的那些问题?
数据冗余:系主任和系名的重复也消失了,总体上冗余更少了。——有改进
插入异常:若要插入一个尚无学生的新系的信息,直接操作系表即可,完全支持。——有改进
修改异常:若李小明转系到法律系,只需要修改一次对应的系名的值即可。——有改进
删除异常:若删除某个系中所有的学生记录,该系的信息不会丢失。——有改进
反范式化
一般说来,数据库只需满足第三范式(3NF)就行了。
没有冗余的数据库设计很容易可以做到。但是,没有冗余的数据库未必是最好的数据库,有时为了提高运行效率,就必须降低范式标准,适当保留冗余数据。具体做法是:在概念数据模型设计时遵守第三范式,然后将降低范式标准的工作放到物理数据模型设计时考虑。
降低范式说白了就是增加字段,允许冗余,达到以空间换时间的目的。
〖例〗:假设有一张订单表,存在 “单价”、“数量”、“金额” 几个非主属性,而 “金额” 可以由 “单价” 乘以 “数量” 得到。显然该表的设计不满足第三范式,因为 “金额” 是冗余字段,它完全函数依赖于属性组(单价、数量),进而 “金额” 对于码(这里未列出)存在传递函数依赖。但是,增加“金额”这个冗余字段,可以提高查询统计的速度,这就是以空间换时间的作法。
PS:在
Rose 2002中,规定列有两种类型:数据列和计算列。像 “金额” 这样的列被称为 “计算列”,而 “单价” 和 “数量” 这样的列被称为 “数据列”。
总结
1NF(第一范式)
1NF 的限定条件如下:
- 每个列必须有一个唯一的名称
- 行和列的次序无关紧要
- 每一列都必须有单个数据类型
- 不允许包含相同值的两行
- 每一列都必须包含一个单值 (一个列不能保存多个数据值,也就是上文提到的“属性不可再分”)
- 列不能包含重复的组
第一范式会存在数据过度冗余,以及更新、删除和插入异常的问题。
2NF(第二范式)
2NF 的限定条件如下:
- 它符合第一范式
- 所有的非键值字段均依赖于所有的键值字段
第二范式也会存在更新、删除和插入异常的问题。
3NF(第三范式)
3NF 的限定条件如下:
- 符合 2NF
- 不包含传递相关性(即,一个非键值字段的值依赖于另一个非键值字段的值)。
符合 3NF 要求的数据库设计,基本上解决了数据冗余过大,插入异常,修改异常,删除异常的问题。当然,在实际中,往往为了性能上或者应对扩展的需要,经常 做到 2NF 或者 1NF,但是作为数据库设计人员,至少应该知道,3NF 的要求是怎样的。
范式化和反范式化的优缺点
范式化
优点:

缺点:

反范式化
优点:

缺点: